在行测考试数量关系中,牛吃草问题一直是广大考生头疼的内容。其实这类题的本质就是追及问题,只需要抓住题干核心,分清“牛吃草的速度”再追“草生长的速度”即可利用公式直接列方程求解。
让我们在一道例题中感受牛吃草问题的“套路”:
【例1】牧场上有一片匀速生长的草地,可供27头牛吃6天,或供23头牛吃9天。那么这片草地可供21头牛吃几天?
【分析】虽然题干描述是不同数量的牛吃同一片草地的情况,但我们应抓住题干核心,将此题理解为追及问题:牛用吃草的方式消耗草地的草量,草用生长的方式增加草量,这片草地被吃完的时刻,即为“牛吃草”追上“草生长”的时刻。用追及问题的线段图表示这个过程如下:
结合追及问题“路程差(即同时出发时的初始距离)=速度差×追及时间”的公式,这里的初始距离很显然是这片草地的原有草量,所以可得公式:
原有草量=(牛吃草的速度-草生长的速度)×时间。
【解析】这道题中不同方案涉及不同数量的牛吃草,每头牛无差别,故:
设每头牛单位时间的吃草量为1,从而牛吃草的速度可直接用牛的数量表示;
设草生长的速度为x,即可直接套用公式得:
原有草量=(27-x)×6
原有草量=(23-x)×9
两式联立可得x=15,可得原有草量=72,再结合问题描述可设这片草地可供21头牛吃t天,可得方程72=(21-15)×t,求解的t=12,所以这片草地可供21头牛吃12天。
通过以上例题的解答过程,我们不难总结出牛吃草问题的解题思路:
1. 理解题意,分清牛和草(牛吃草消耗草量,草生长增加草量);
2. 设每头牛单位时间的吃草量为1,草生长的速度为x,结合公式“原有草量=(牛吃草的速度-草生长的速度)×时间”列方程求解草生长的速度x、原有草量;
3. 结合问题再次代入公式求解。
接下来为大家送上一道变式练习题小试牛刀吧!
【练习】快递公司原有一批积压件未派送,以后每天都有相同数量的新收件需派送,且快递公司的每个派送员每天的派件数相同;如果每天4个派送员派件,则第9天恰好无积压件;如果每天5个派送员派件,则第6天恰好无积压件。那么3个派送员派件需要几天?
A.17
B.18
C.19
D.20
【解析】题干涉及派送员派件(积压件),快递员在消耗积压件,故派送员对应“牛”,通过“每天都有相同数量的新收件需派送”可得,新收件使得积压件增加,新收件对应“草”,故设每个派送员每天的派件数为1,每天新收件的数量为x,可得原始积压件=(4-x)×9=(5-x)×6,解得x=2,原始积压件=18,结合问题,设3个派送员派件需要t天,可得18=(3-x)×t,解得t=18,故选B。


 更多黑龙江省考行测技巧与方法扫码获取
更多黑龙江省考行测技巧与方法扫码获取
 行测数量关系技巧方法案例
行测数量关系技巧方法案例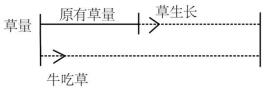
 行测数量关系备考提醒
行测数量关系备考提醒

 行测数量关系技巧还没掌握?扫码回复“咨询老师”
行测数量关系技巧还没掌握?扫码回复“咨询老师”